I found a nice puzzle in the newspaper (Logelei, Zeit Magazin Nr.4 22.1.2015). It has (like many puzzles) the structure of a constraint satisfaction problem:
There are strange traffic rules in the country Leepf. At every crossing there is a sign with an arrow and a number. The number indicates the number of distinct numbers that are found at crossings in this direction.
Given is a grid of 5x5 crossings with 4 numbers already filled in:
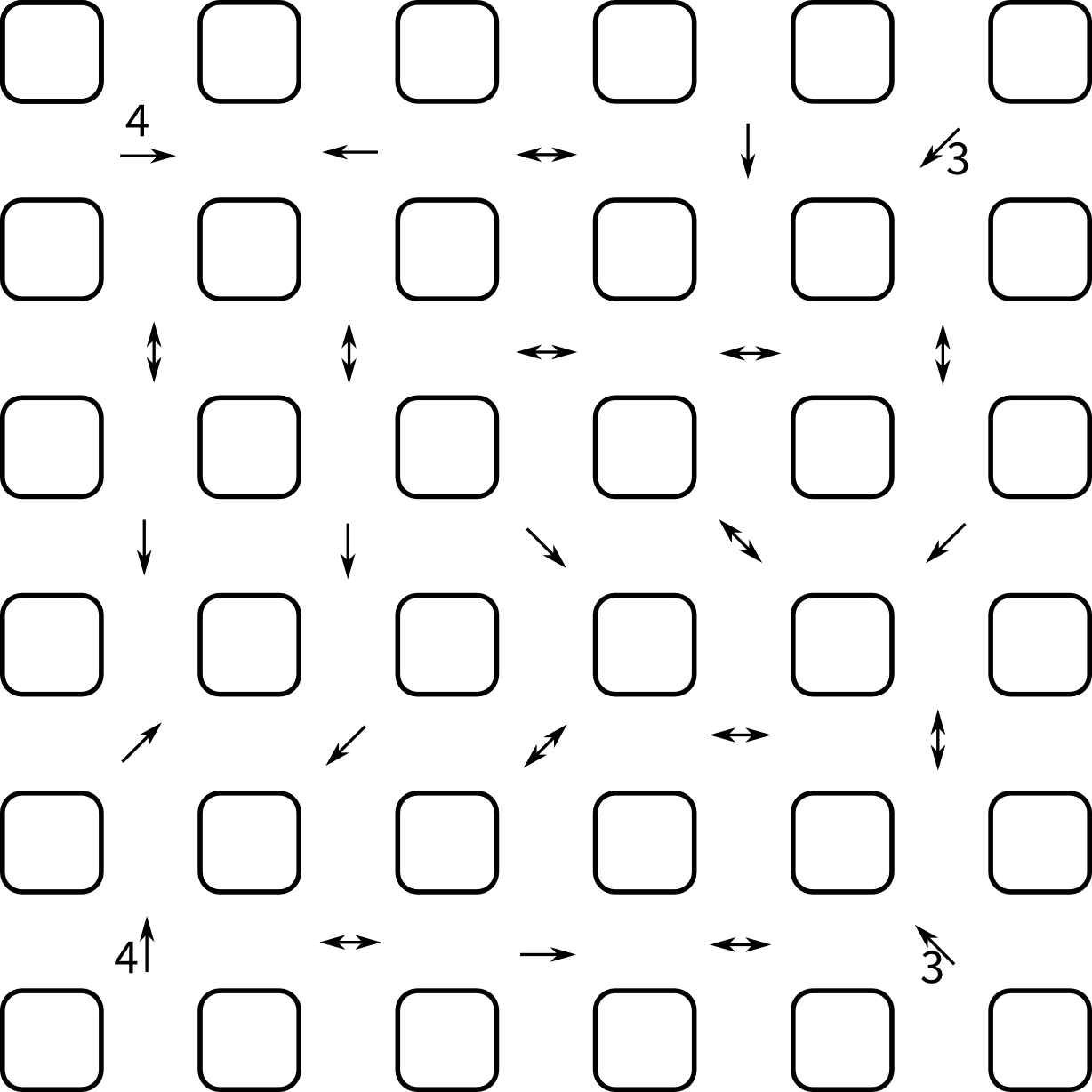
Given my recent interest in constraint satisfaction, I immediately tried to solve it with constraining order, which turns out to be straightforward.
A new type of Constraint needs to be implemented that relates the value of a variable with the number of distinct values in a list of variables. I initially forgot to flag a labeling as inconsistent when not all variables in the list are labeled and there are not enough of these to reach the target number of distinct values. It turned out to help performance quite a bit by being able to reduce the problem space a bit at the beginning and stop examining some partial labelings earlier during backtracking.
The most tedious part is the formulation of the constraints, as there are 25 of them and they must be hardcoded. I used a numpy array to hold the variables in the same layout as the crossings, this allows to make use of the better slicing to conveniently express the constraints.
The full script looks like this:
from constrainingorder.sets import DiscreteSet
from constrainingorder.variables import DiscreteVariable
from constrainingorder.constraints import Constraint, FixedValue
from constrainingorder.solver import solve,ac3
from constrainingorder import Space
import numpy as np
"""
This script solves the following puzzle (Logelei, Zeit Magazin Nr.4 22.1.2015):
There are strange traffic rules in Leepf. At every crossing there is a sign
with an arrow and a number. The number indicates the number of distinct
numbers that are found at crossings in this direction.
Fill in the missing numbers
For the layout of crossings see crossings.svg
"""
class NDistinctEqual(Constraint):
"""
This constraint makes sure that the value of a variable is equal to the number of distinct values in a list of variables.
"""
def __init__(self,var,varlist):
domains = {}
domains[var] = var.domain
for v in varlist:
domains[v] = v.domain
Constraint.__init__(self,domains)
self.var = var
self.varlist = varlist
def satisfied(self,lab):
if not self.var.name in lab:
return False
values = set([])
for var in self.varlist:
if not var.name in lab:
return False
values.add(lab[var.name])
return len(values) == lab[self.var.name]
def consistent(self,lab):
if not self.var.name in lab:
return True
values = set([])
unknown = 0
for var in self.varlist:
if not var.name in lab:
unknown += 1
continue
values.add(lab[var.name])
#cannot reach number
if len(values) + unknown < lab[self.var.name]:
return False
#exceed number
if len(values) > lab[self.var.name]:
return False
return True
#set up variables
domain = DiscreteSet(range(1,5))
crossings = []
for i in range(5):
row = []
for j in range(5):
name = "c%d%d" % (j,i)
row.append(DiscreteVariable(name,domain=domain))
crossings.append(row)
crossings = np.array(crossings)
#set up constraints
cons = []
cons.append(NDistinctEqual(crossings[0,0],crossings[0,1:]))
cons.append(NDistinctEqual(crossings[0,1],crossings[0,:1]))
cons.append(NDistinctEqual(crossings[0,2],crossings[0,(0,1,3,4)]))
cons.append(NDistinctEqual(crossings[0,3],crossings[1:,3]))
cons.append(NDistinctEqual(crossings[0,4],crossings[(1,2,3,4),(3,2,1,0)]))
cons.append(NDistinctEqual(crossings[1,0],crossings[(0,2,3,4),0]))
cons.append(NDistinctEqual(crossings[1,1],crossings[(0,2,3,4),1]))
cons.append(NDistinctEqual(crossings[1,2],crossings[1,(0,1,3,4)]))
cons.append(NDistinctEqual(crossings[1,3],crossings[1,(0,1,2,4)]))
cons.append(NDistinctEqual(crossings[1,4],crossings[(0,2,3,4),4]))
cons.append(NDistinctEqual(crossings[2,0],crossings[3:,0]))
cons.append(NDistinctEqual(crossings[2,1],crossings[3:,1]))
cons.append(NDistinctEqual(crossings[2,2],crossings[(3,4),(3,4)]))
cons.append(NDistinctEqual(crossings[2,3],crossings[(0,1,3),(1,2,4)]))
cons.append(NDistinctEqual(crossings[2,4],crossings[(3,4),(3,2)]))
cons.append(NDistinctEqual(crossings[3,0],crossings[(2,1,0),(1,2,3)]))
cons.append(NDistinctEqual(crossings[3,1],crossings[(4,),(0,)]))
cons.append(NDistinctEqual(crossings[3,2],crossings[(4,2,1),(1,3,4)]))
cons.append(NDistinctEqual(crossings[3,3],crossings[3,(0,1,2,4)]))
cons.append(NDistinctEqual(crossings[3,4],crossings[(0,1,2,4),4]))
cons.append(NDistinctEqual(crossings[4,0],crossings[:4,0]))
cons.append(NDistinctEqual(crossings[4,1],crossings[4,(0,2,3,4)]))
cons.append(NDistinctEqual(crossings[4,2],crossings[4,(3,4)]))
cons.append(NDistinctEqual(crossings[4,3],crossings[4,(0,1,2,4)]))
cons.append(NDistinctEqual(crossings[4,4],crossings[(0,1,2,3),(0,1,2,3)]))
cons.append(FixedValue(crossings[0,0],4))
cons.append(FixedValue(crossings[0,4],3))
cons.append(FixedValue(crossings[4,0],4))
cons.append(FixedValue(crossings[4,4],3))
space = Space(crossings.ravel().tolist(),cons)
ac3(space)
for vname, domain in sorted(space.domains.items()):
print vname, domain
for solution in solve(space,method='backtrack'):
print solution
This gives a single, correct solution very quickly. I had the impression that the solution is quite heavily constrained even without the given number, so I removed the FixedValue constraints and solved again. This resulted in only 14 solutions. The simplest one has value 1 for every variable, which one could have found by careful thinking. Most of the other solutions only contain the values 1 and 2, and then there are one which contains the values 1 to 3 and one that contains the values 1 to 4. So the 4 given numbers are more than enough information to make the solution unique, either one of them would have been enough, but also a tad more difficult. Mentioning that there is a four somewhere would also be ok, but even more difficult.