The eight queens problem is a classic:
How to place eight queens on a standard 8x8 chessboard in such a way that they can not attack each other?
It was first posed in 1848 by M. Bezzel, and the great C.F.Gauss worked on it (however, he only found 72 of the 92 possible solutions, and although he claimed that there are 92, he did not prove it). The generalisation to larger board sizes is then called the n queens problem, for which there are even some (more or less) practical applications. For a really great review about the n queens problem, its generalisations, known results, open questions and a lot of historical background, see [1]. It is also an interesting testing field for algorithms. For an overview over different algorithms, see [2].
It is also a classic for teaching programming, where it is often used as an problem of medium complexity and to introduce the techniques of backtracking and recursion. This is where I was exposed to it again, when I was helping with a programming course. It is surprisingly difficult for students to understand recursion and even more to apply it themselves.
At that time I was reading in yet another classic, but one which is much less well known and also much less relevant today. It is a book about the numerical evaluation of multiple integrals [3], dating from 1971, a time, where computers where slow and computing time was expensive, and therefore it was necessary to put some thought into doing things as cheap as possible. Really high dimensional integrals still are a problem today, and some of the standard tools that are used today ((Quasi) Monte Carlo Methods), are already mentioned there, while others are not (Sparse grids).
When I skimmed the chapter about Quasi Monte Carlo Methods (there called "Number theoretical methods"), I stumbled upon a figure, where the location of evaluation points for a QMC method for the unit square was shown:
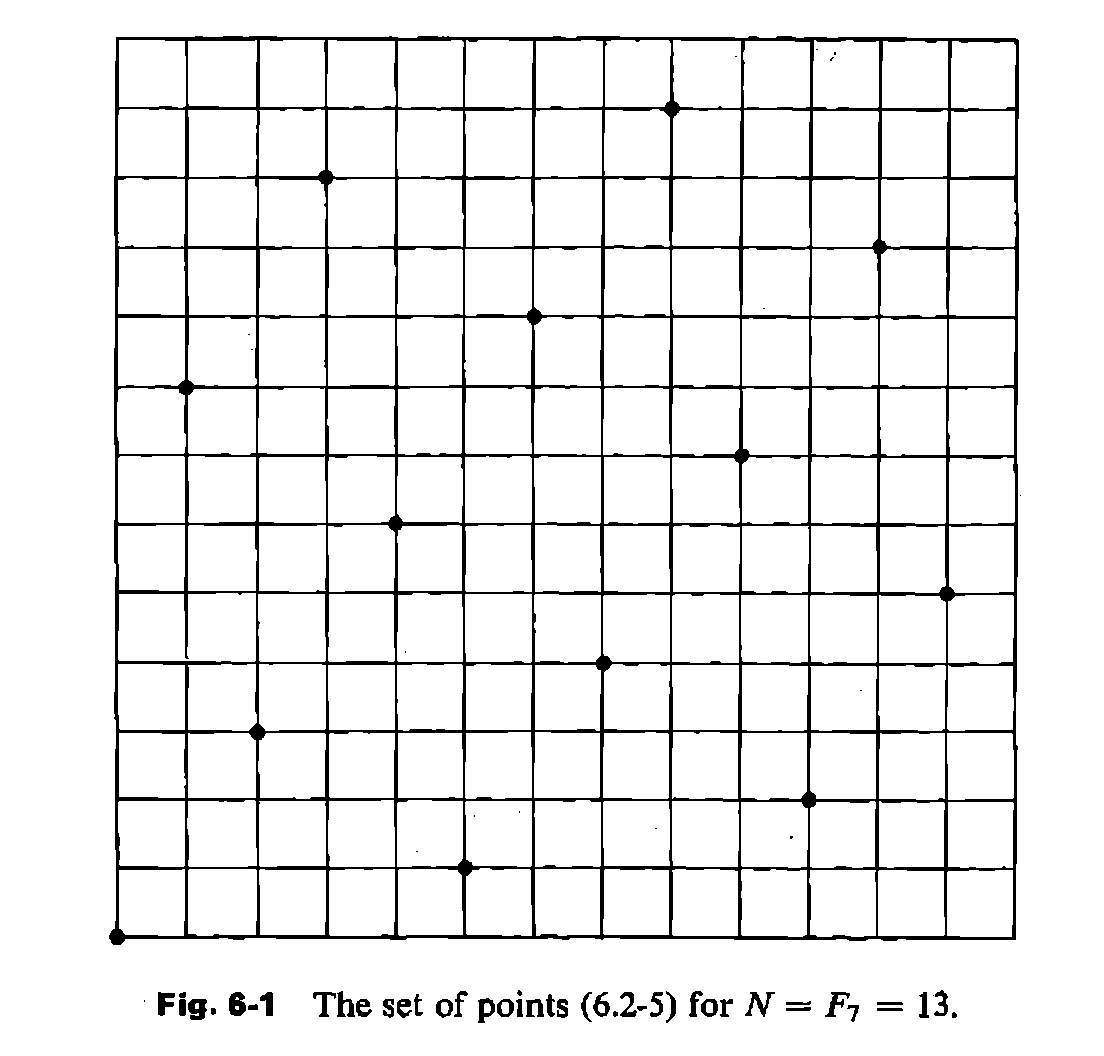
This is a solution for the 13-queens problem! The sequence of evaluation points is given as a prescription that is based on another classic: The fibonacci numbers $F_n$.
I immediately wrote a short program to test whether this sequence generates solutions to the respective queens problems for all fibonacci numbers. This was not the case. But it did for $F_m$ with $m \mod 6 = \pm 1$, for all $m$ that I tested. These are the odd fibonacci numbers with odd index [5]. The one queen problem is trivial, and the two and three queens problem is unsolvable, so it works only for $F_m geq 5$. I then decided to try to prove this.
To prove this one has to show that the m points given by the above formula have the follwing properties
- all of them must have different x values (column)
- all of them must have different y values (row)
- the sum of x and y must be different for all points (diagonal in one direction)
- the difference of x and y must be different for all points (diagonal in other direction)
The first one is trivial, the second one easy if one knows that
The third and fourth are not obvious (at least they were not obvious to me).
At one point my spirit fell, when I discovered, that the first few Fibonacci numbers (those that I tested) with this property are the fibonacci primes [4]. For those it is not surprising to fulfull the conditions above. But to my relief, it turned out, that the construction also solves the 4181 queen problem, even though 4181 is not a prime number.
I asked a friend of mine, who does mathematics, but he only mumbled something about "structure of unities in the quotient ring of the integers module the ideal generated by the m-the fibonacci number".
Then I sat down with another friend who does computer science, and together we were able to prove it in one afternoon. The proof for the central theorem is described here, for those that want to try to reproduce the proof. This property is quite surprising, because it gives information about the gcd of the successor of a number.
I just found another paper about an interesting property of the fibonacci numbers [6], which might or might not be connected to this. It seems that if you want to find interesting properties and try to prove them, the fibonacci numbers seem to be a good target.
| [1] | Bell, J. & Stevens, B. A survey of known results and research areas for n-queens Discrete Mathematics, 2009, 309, 1 - 31 |
| [2] | https://sites.google.com/site/nqueensolver/home/algorithm-results |
| [3] | Stroud, A. Forsythe, G. (ed.) Approximate Calculation of Multiple Integrals Prentice Hall, 1971 |
| [4] | http://oeis.org/A005478 |
| [5] | http://oeis.org/A190949 |
| [6] | Tanya Khovanova, http://arxiv.org/abs/0712.3509 |