When you look at an average webpage, chances are very high, that your computer loads one or more JPEG images. A image saved in the JPEG Format usually takes between 30 and 150 times less memory than a uncompressed image, without looking much different.
The reason why images (and music and many other things) are so well compressible has to do with sparsity. Sparsity is a property of signals in a vectorspace with a basis, but in contrast to many other properties it is difficult to tackle within the framework of linear algebra. In this post I want to write a bit about signals, vectorspaces and bases, about sparsity and about a very cool technique that I discovered recently.
Signals and vectorspaces
If you want to represent a image in the computer, one of the possibilities is, to divide it into small rectangular regions, call these pixels, and then use numbers for each pixel to describe its color. In the case of a grey scale picture, a single number per pixel suffices. We can now write down these numbers one after the other, and end up with a long string of numbers, representing a image.
Now something differnt: From school you might know the concept of a vector. It is usually represented by a arrow pointing from the origin to some other place, together with a $x$ and $y$ axes:
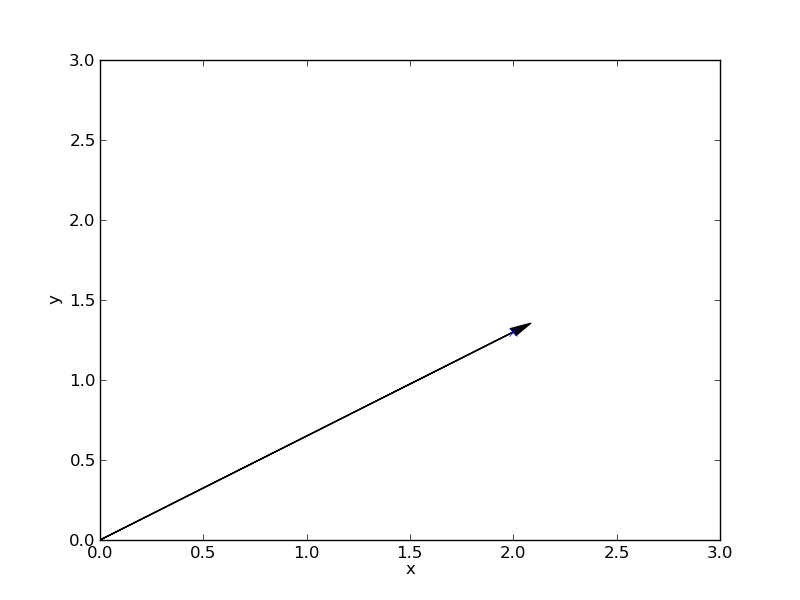
The vector can also be described as a pair of numbers, like this
If you start out at the origin, the upper and lower numbers tell you, how far you have to go in the direction of the $x$ and $y$ axis to arrive at the point the vectors pointing to. The two numbers are called coordinates, the corresponding axes are called coordinate axes. Because there are two of them, one calls this a two-dimensional vectorspace. But one needs not to stop there, one could have three coordinate axes, then the arrows would point to places outside the screen plane, and we would need three numbers.
Or we could have several million axes, then it is difficult to imagine an arrow, but we could still work with it by writing down several million coordinate values. Just like the image I talked about earlier could be represented by a few million numbers. So we could think about the image representation as a vector in a high dimensional vector space.
In fact many things can be represented as long strings of numbers, e.g. sounds, time series, and many more. To make general statements about all these things, they are given the name signal. For example: A signal is a vector in a (usually high dimensional) vector space.
Sparsity and bases
A signal is called sparse, if only a few of its coordinates are nonzero, and most of them are zero. Below I show an 2D example of a number of sparse signales, because in 2D one can draw arrows. A sparse signal in 2D is located on one of the coordinate axes. I have shifted the origin to the middle of the plot and suppressed the arrows, otherwise it would be a very crowded plot.
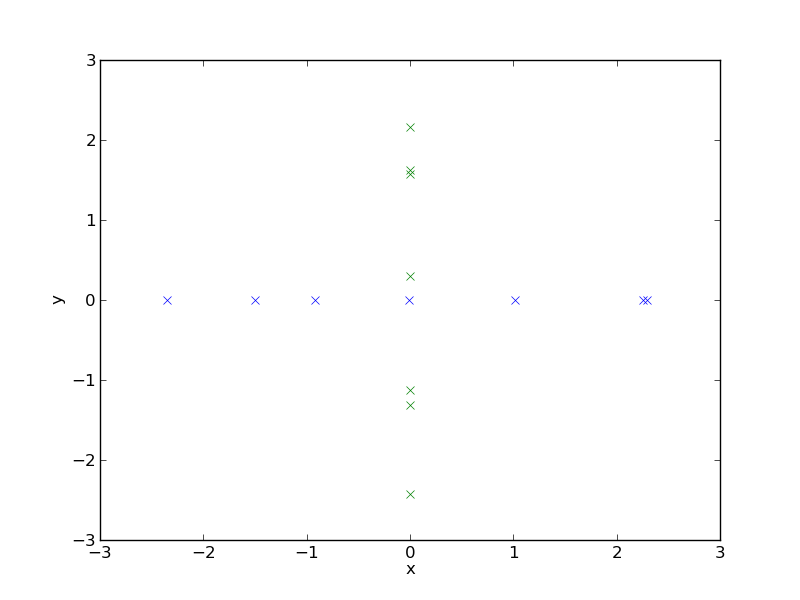
Usually this is not the case with images, because the numbers we use to describe the grey value of a greyscale picture are zero only when the pixel is black. So a black picture with only a few brighter spots would be sparse.
The coordinate values tell us, how far we have to go in the direction of the corresponding coordinate axis. So what happens if we just use a different set of coordinate axes.
A set of coordinate axes is called basis. The same vector has different coordinates when expressed in a different basis. The $x$-$y$ axis we have used until now is called the standard basis. If one knows the coordinates of a vector in one basis, one can caluclate the coordinates with respect to another basis (transform the vector). This is easy, but I will not explain that here.
So can we make a signal sparse by changing the basis. The answer is yes. Here is an example of a number of vectors, that have nonzero coordinates in the standard basis, but when we change to the basis given by the two arrows, they become sparse
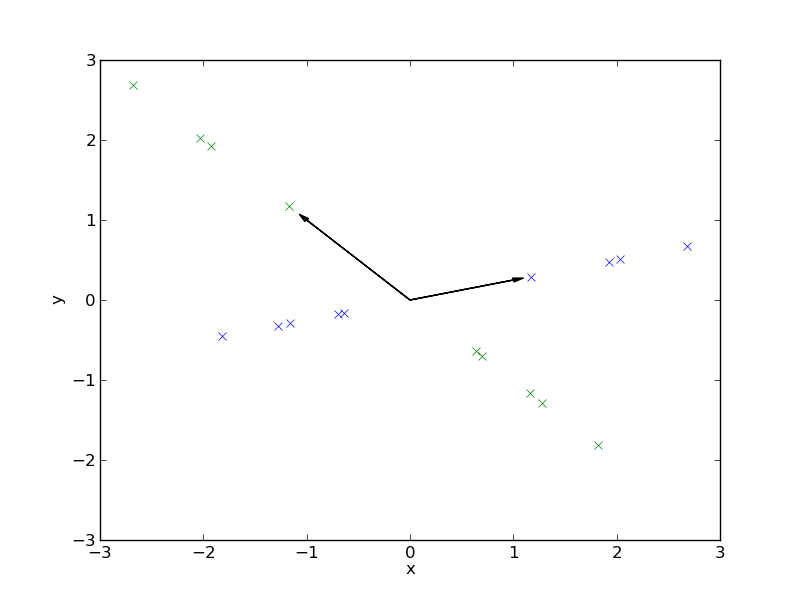
So sparseness is a property for a collection of signals expressed in a basis. A signal can be sparse in one basis and non-sparse in another. But for every basis there are signals that are not sparse.
So for the case of images, there could be a basis in which (good approximations to) images are sparse, despite the fact, that images are not sparse in the standard basis. However, if we expressed a piece of music or a time series in this basis, it probably would not be sparse. And there are indeed bases in which images are sparse, like the DCT base or the wavelet base.
So looked at it in yet another way, a set of signals is sparse in a basis, if they are located on coordinate axes and other low-dimensional subspaces.
Sparsity is difficult for linear algebra, because in linear algebra one is concerned with all possible vectors, and sparsity is a property that can only hold for a subset of all vectors.
Compression
It is of course great when we know a basis in which a signal is sparse. We then only have to store which coefficients are nonzero and what their value is, which can usually be accomplished with less storage than storing a non-sparse representation.
Of course, a basis transform into a good basis is only one of the steps performed in modern-day formats like JPEG. There are other techniques like prediction schemes, entropy coding and quantisation that play an important role for the overall compression performance.
Compressed sensing
A few weeks ago I read an newspaper article about a revolutionary development for digital cameras. It talks about a camera that has only one single pixel sensor abd can take blurry pictures, but needs 10 minutes to take a picture, and something about compression. And I did not understand what exactly with this camera is supposed to be the revolution. So I read the original scholarly articles that were linked, and found out that there indeed is a very cool idea behind all that, but the newspaper article completely missed the point. And this camera is only a proof of concept of this really cool idea.
A standard digital camera works roughly like this: The objects you want to photograph emit light, and the lenses make sure that this light hits a CCD sensor array in the back of the camera. This sensor array has a sensor for every pixelof your final image. So in other words, each sensor measures the coordinate of the signal corresponding to his pixel in the standard basis. And the CCD array can do several million measurements in parallel in a tiny fraction of a second.
If we look at the measurement in terms of vector spaces, a measurement corresponds to a scalar product of the signal with a measurement vector $\mathbf{m}_i$, yielding a single number $m_i$. The measurements of a standard digital camera correspond to projections on the coordinate axes:
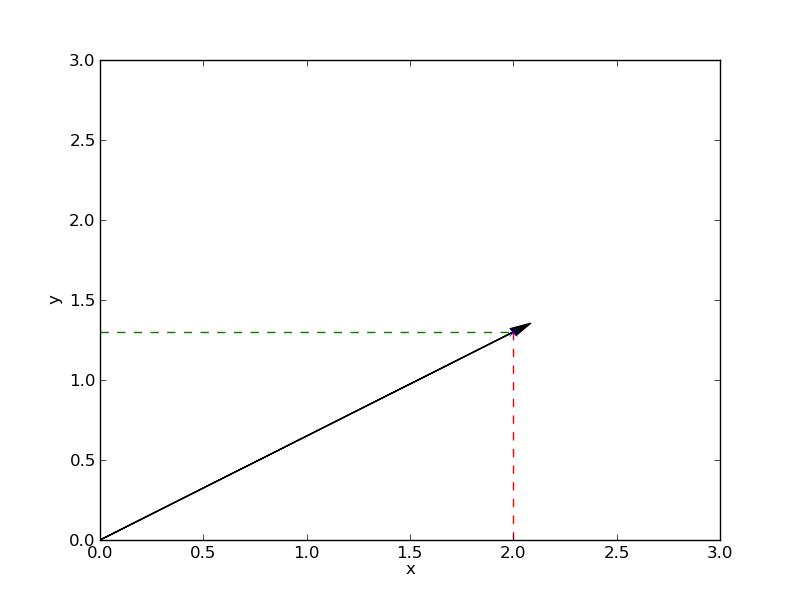
But we know that we only need a few nonzero coordinates to represent a picture, because we know a basis, in which the image signal is sparse. So the question is, can we in principle measure the few nonzero coordinates directly, instead of measuring many pixels, and afterwards transforming to a sparse representation.
It turns out the answer is yes. One can obtain a picture with many pixels by making much fewer measurements with appropriately chosen measurement vectors, because we know that the signal is sparse in a certain basis. The reconstruction is more difficult and requires more computation, but it is still feasible. This technique is called compressed (or compressive) sensing, and this is indeed a very cool idea.
I looked a bit into the literature and there is very deep and apparently very beautiful mathematics behind that, and everyone is pretty excited. It is quite funny, because years back in university in a course I gave a presentation about one of the central algorithms in the reconstruction part. A good overview over compressed sensing is in this paper, the digital camera is described here.
Of course, a digital camera is not the best example for that because it is very easy to make a few million measurements in parallel, so the measurement part is not the bottleneck. However, for example with other applications like MRI, the bottleneck is indeed the measurement, and compressive sensing gives impressive improvements.
A magical compressive sensing game
Maybe you know the game Mastermind. A variation of this might be the following game (lets call it SparsterMind). It is played on a board not unlike the Mastermind board, but with 100 holes. The codemaster places a small number of colored pegs in some of the slots. He can choose how many pegs he places, but not more than 3. Different colors are worth different numbers of points, some colors have negative values. The game then progresses in rounds.
- The code breaker marks some holes on his side of the board with white pegs.
- The code master indicates the total score of the indicated holes
The game goes on for 20 rounds or so. If the code breaker has not guessed the correct holes and colors of the codemaster, he looses, otherwise he wins.
On first sight this seems very difficult, but with the knowledge about compressed sensing that we have, we can see, why it is possible. We think about the pegs in the holes as a high dimensional, yet sparse vector, the coordinate value corrsponds to the score of color of the peg. Each round is a measurement. Now we know that with compressed sensing it is possible to recover the signal with much less than 100 measurements.
The compressive sensing strategy might be not easy to play for humans, because one has to solve large linear optimisation problems, but a computer can do it very easily. I implemented this game in python and put it on github, so you can be the codemaster and see how the computer figures it out.