Have you noticed that a bicycle leaves two traces when it drives through snow or mud? This is because the front- and backwheel do not follow the same paths. The same type of motion applied for a car with a trailer with one axle (if the trailer has two axles, than the situation is more complicated), a boat towing a smaller boat or generally when one object (we will call it leader) moves, and another object (follower) follows at a fixed distance. In this post I want to show how to calculate the trajectory of the follower for a given trajectory of the leader.
We represent the path of both leader and follower by a pair of functions, giving the x and y coordinates for a given point in time. Since we are only interested in the path (the traces in the mud) these functions are not unique. One can move as slow or fast as one wants at any point of the trajectory, the trajectory of the follower only depends on the trajectory of the leader and its starting position. Each imaginable way in which the leader can move along the trajectory (e.g. pretty fast for the first 10m, then slowing down for 5m and then fast again) corresponds to a pair of such functions. This is why one speaks of parameter representation of a curve, but I find it easiest to think about time as the parameter. I will only talk about time in what follows.
As all considerations are independent of the dimension, I will write $\mathbf{L}(t)$ for a vector whose entries are the functions giving the coordinates for the position of the leader. Similarly I write $\mathbf{F}(t)$ for the position of the follower. The vector with the derivatives of the coordinates with respect to time will be called $\dot{\mathbf{F}}(t)$ and $\dot{\mathbf{L}}(t)$
We want to obtain an equation for the parameter representation of the path of the follower in which the parameter representation of the leader enters. There are two two conditions that must be fulfilled:
- The direction condition: At each point in time the velocity of the follower must point in direction of the leader. This can be written as the following equation, where $\alpha$ is yet-to-be-determined proportionality factor. $$\mathbf{F}(t) = \alpha (\mathbf{L} - \mathbf{F})$$
- The distance condition: At each point in time the distance between leader and follower mustn't change. This can be enforces by $$(\dot{\mathbf{L}} - \dot{\mathbf{F}}) \cdot (\mathbf{L} - \mathbf{F}) = 0$$ The dot denotes a scalar product between the two vectors. It is not obvious that this makes the distance between leader and follower constant. This equation basically says that the relative difference vector and the relative velocity vector must be orthogonal, just as in the motion of an object around a center. One can think about the above equation restriction the relative velocity to rotations of the follower around the leader (or the other way round, just as you prefer to think about it).
The two conditions can be combined into a single equation, which I will call henceforth the bicycle equation:
This is a difficult equation , namely a coupled system of nonlinear ordinary differential equations, and in most cases it can not be solved analytically (at least I can not do it). But there are several simple examples that can be used to check the equation for plausibility.
For example imagine the bicycle going completely straight in one direction. Then $\dot{\mathbf{L}}$ and $\mathbf{L - F}$ are colinear, the square of the absolute value of the distance cancels and we get
which is exactly what must come out. The backwheel moves in the same direction with the same velocity as the front wheel.
Or imagine an especially skilled cyclist that goes around in such a tight circle, that the backwheel coincides with the center of this circle. Then $\dot{\mathbf{L}}$ is orthogonal to the relative distance vector and we find that the backwheel does not move at all (of course it moves, but in an ideal world it would leave only a single point as trace in the snow, which is what we are calculating).
For more interesting cases it is necessary to solve the bicycle equation numerically with the help of a computer. For those that know about the numerical solution of ordinary differential equations: Eulers method is sufficient. Then we think of a sufficiently smooth path for the front wheel, and let the computer calculate the path of the back wheel.
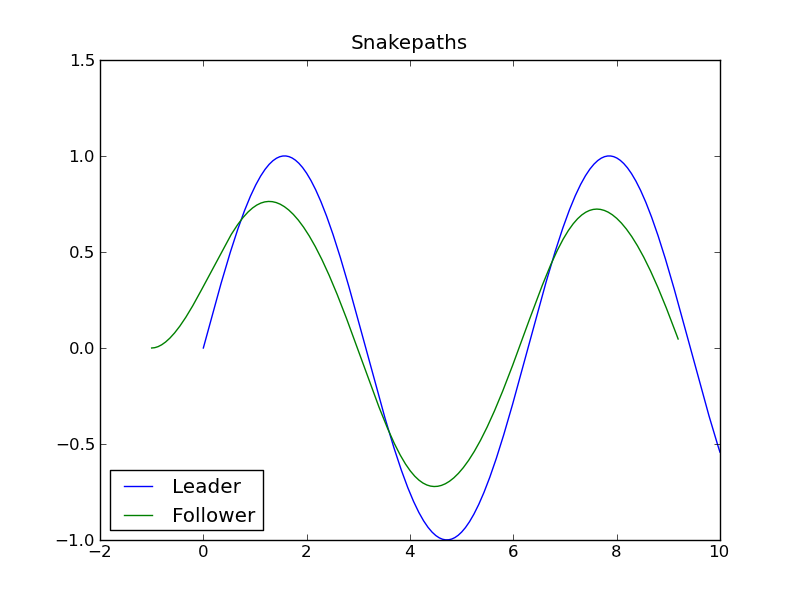
The result for driving in a serpentine pattern can be found in the picture below. The resulting paths look like those that can be found in snow or mud. The follower (back wheel) cuts the corners, therefore the amplitude of the oscillation is smaller. How much smaller it is depends on the length of the bike.
This equation also holds when the leader in behind the follower with respect to the direction of movement. This occurs in situations like driving backwards with a trailer, or pushing a shopping car. That the former is pretty difficult is clear for everyone who has ever tried it.
Below is an example for the serpentines, but with the follower (green) initially in front of the leader (red). But this is a very unstable situation, so they switch places again pretty fast.
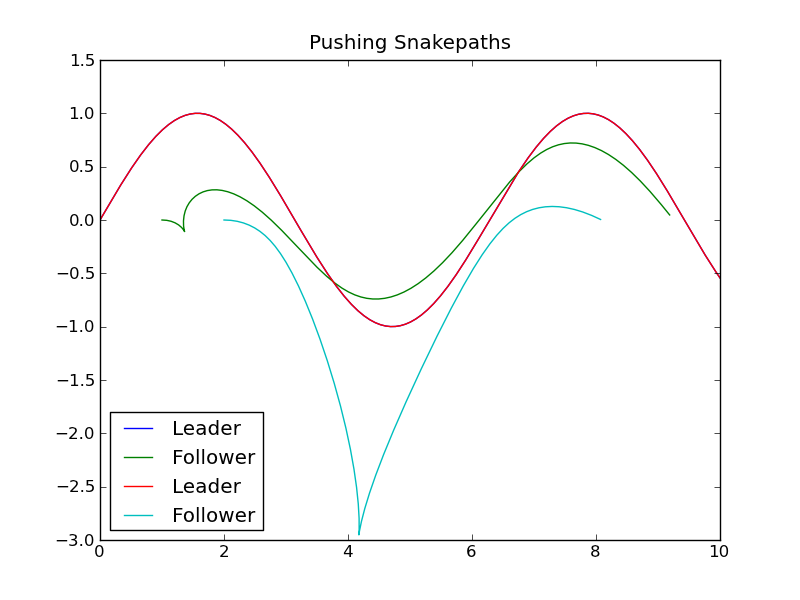
It is this instability that makes driving backwards with a trailer so difficult. The instabilities must be corrected all the time, otherwise something like in the picture happens. Driving a shopping cart (where the front wheels is the follower) is easier, because the long distance to the front wheels makes the system less unstable. In the picture above, the second curve (turquoise) corresponds to a situation where the follower is initially placed three lenght units in front of the leader. You can see that it takes much longer for them to switch places. Also the long distance to the front wheels allows you to steer much more precisely.
So now that you have seen how to attack this problem, you are invited to think of interesting situations for bicycle paths. Maybe you even try to derive the equation for a two axle trailer.
