In this post I will talk a bit about a family of data structures that can be used to efficiently store a set of strings. Later I will present [Liang]'s Method of syllabification that makes use of these data structures. Even more details can be found in the reference given at the end of this post.
Trie
A trie is a tree datastructure for a set of strings, or a associative array that maps strings to values. To determine whether a string is an element of the set one starts at the root of the tree and then at each level takes the branch that is associated with the corresponding letter of the string. If at some point this branch does not exist, than the string is not in the set. If we run out of letters and the current node is marked as a leaf node, then the string is in the set. This results in a very compact representation, as several words can share identical prefixes. An associative array can be realised by attaching values to the leaf nodes.
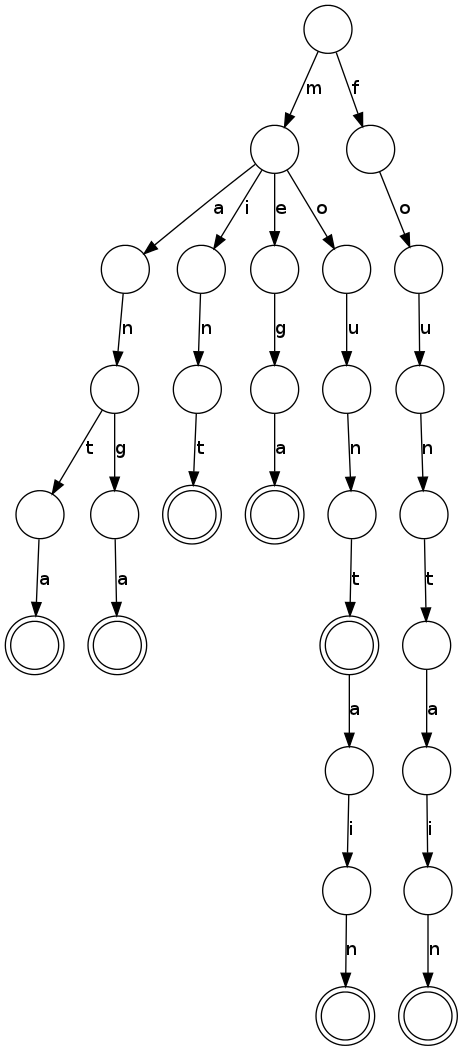
So here is an example, a trie storing 8 words with a total of 43 characters in 29 nodes. Double circles are the leaf node. Can you find all the words?
Radix Trie
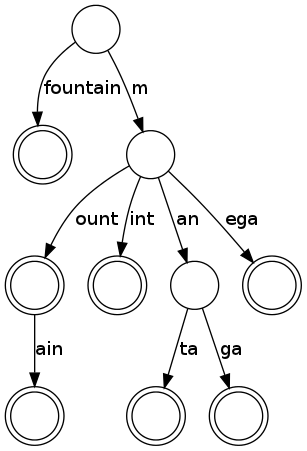
But one can do a more few optimizations. In the trie above we notice a large number of nodes with only one child, that form long chains. If we merge these nodes, the data structure is called Patricia Trie or Radix Tree. This merging reduces the number of nodes and the memory overhead significantly, especially for few entries. A radix tree for the same entries as above is shown below. It requires only 10 nodes.
Suffix Compression
The trie achieves its space efficiency by sharing identical prefixes of words. One possibility to increase the efficiency even further is to also share identical suffixes. This can be done by merging leaf nodes and their parents when possible. The Trie with suffix compression only takes 20 nodes, the Radix Tree only 5 nodes.
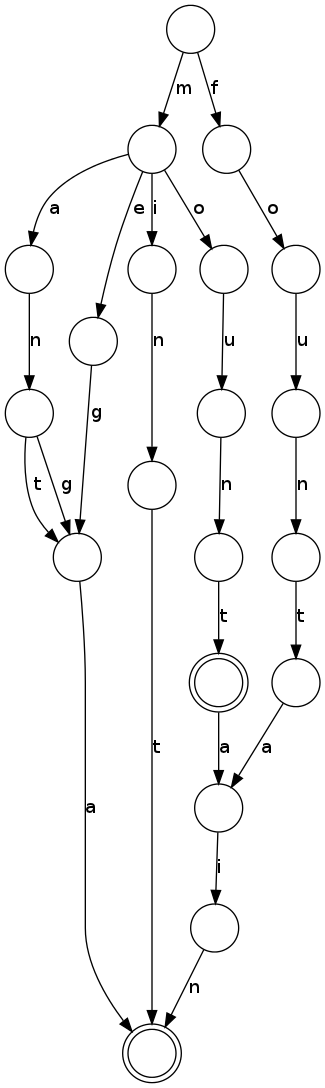
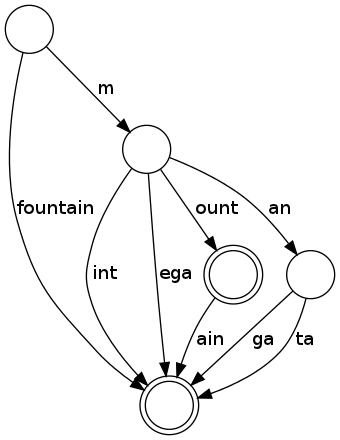
In practice, the tree structure can also be laid out cleverly in memory in a continuous block of memory to be very space efficient, but this is a rather technical procedure.
Liangs Method
In the method of [Liang] hyphenation patterns are used to determine possible hyphenation points. A few example for a hyphenation pattern are
4m1p pu2t 5pute put3er o2n on1c 1ca 1na n2at 1tio 2io pr2 1gr
Odd numbers indicate an allowable position for an hyphen, so the last pattern tells us that a hyphen can go before the letters gr, unless another pattern with a larger even number forbids this hyphen.
In total there are around 5000 such patterns, and trie is used to store all the hyphenation patterns in a very space efficient manner and allow very fast lookup. For the small set of patterns shown above the trie looks like this:
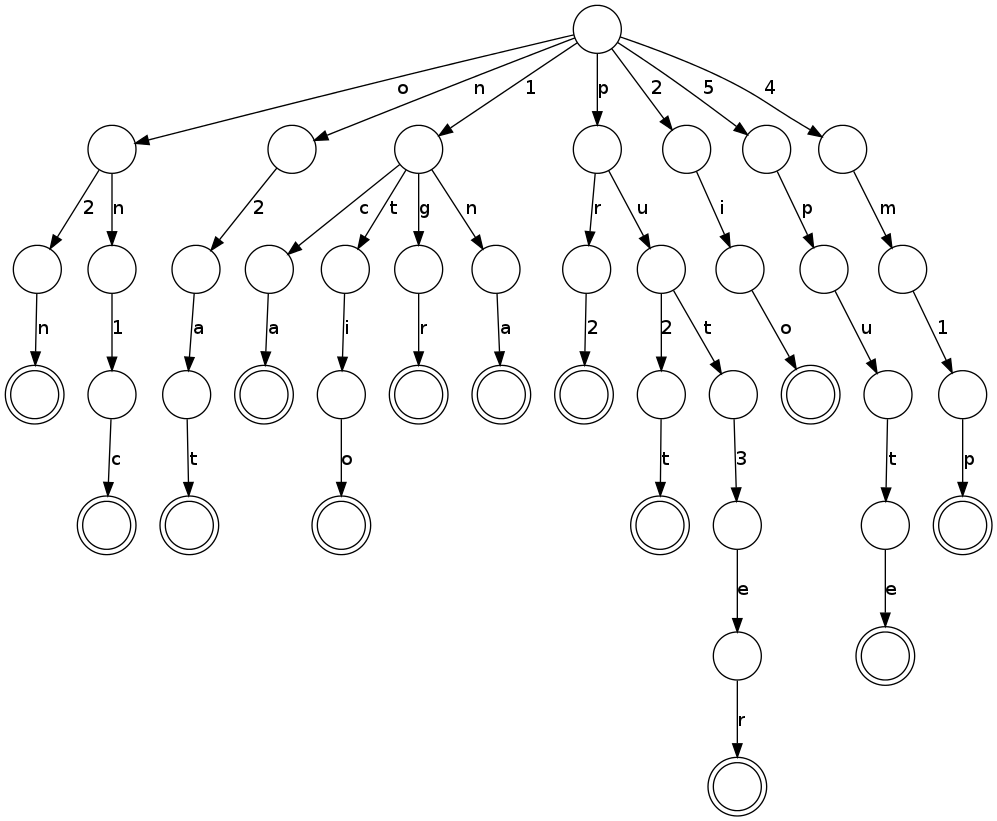
To determine a possible hyphenation for a word, e.g. 'computer', we look for matching patterns starting with every letter of the word, and note the numbers:
| letter | Matches |
|---|---|
| c | no match |
| o | no match |
| m | 4m1p |
| p | pu2t, put3er, 5pute |
| u | no match |
| t | no match |
| e | no match |
| r | no match |
So in total we get co4m5pu2t3er, as the 1 from the m match is overridden by the 5 from the p match. All odd numbers indicate places, where hyphens can go, so com-put-er.
The patterns are generated such that all found hyphens are correct, even if not all possible hyphens are found. So if we use this method to count syllables, we underestimate the total number. But usually enough positions are found to neatly layout a given text in a paragraph.
In the next post I will give an overview over another algorithm for syllabification, called IGTree, and the data structure used in this algorithm
| [Liang] | (1, 2) Liang, F. M. Word Hy-phen-a-tion by Com-put-er Stanford University, Department of Computer Science, 1983 |